A lot of medieval astrological techniques involve knowing the “Lord of the Day” and the “Lord of the Hour”, which are simply the planet ruling the current day, and the planet ruling the current hour respectively. This article will explain how to calculate these – including how to look at a chart and work it out in your head!
Lord of the Day is very easy if you already know the day – and was even easier in medieval times when scholars wrote in Latin, because in Latin the days of the week were named after planets. That’s still true in modern Romance languages – in French, Friday is “Venredi” which means “Venus’ day”, Tuesday is “Mardi”, which is Mars’ day and so on.
This means Lord of the Day is trivial to work out – if it’s Wednesday today, the Lord of the Day is Mercury. However, if you have a chart in front of you that just tells you the date but not the day – don’t panic! You can still work it out in your head – see the section below.
| English | Latin | Planet |
| Sunday | Dies Solis | Sun |
| Monday | Dies Lunae | Moon |
| Tuesday | Dies Martis | Mars |
| Wednesday | Dies Mercurii | Mercury |
| Thursday | Dies Iovis | Jupiter |
| Friday | Dies Veneris | Venus |
| Saturday | Dies Saturni | Saturn |
Lord of the Hour is a bit more fiddly.
While the modern definition of an hour is one twenty-fourth of a day (from midnight to midnight), there were two definitions of the term “hour” in the twelfth century. The usual definition was that the period from sunrise to sunset was divided into twelve equal diurnal hours, and the period from sunset to the following sunrise was divided into twelve equal nocturnal hours.
The length of an hour would, then, depend on your location, the time of year, and whether it was day or night. To give an example, at the summer solstice in Hereford on the English/Welsh border, there are 16 hours and 40 minutes of daytime (between sunrise and sunset), and 7 hours and 20 minutes of night-time (between sunset and sunrise). A diurnal hour at the solstice would, therefore, be 83 minutes and 20 seconds, and a nocturnal hour would be 36 minutes and 40 seconds.
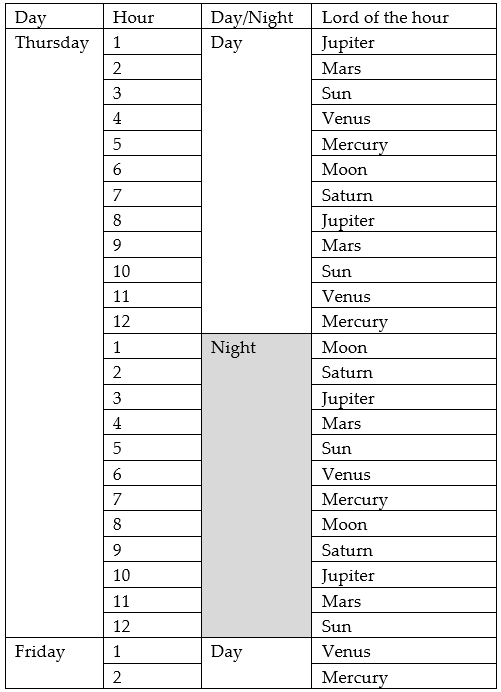
At the equinoxes, daytime and night-time are equal, and the hour is 60 minutes. Thus these hours – the division used today of the day into twenty-four equal hours – were called equinoctal hours. The principle of a planetary hour is that at sunrise on a particular day, the planet ruling the day was also the planet ruling the first diurnal hour. For example, the first diurnal hour of Thursday (Jupiter’s day) is ruled by Jupiter. The second hour is ruled by the next planet in the Chaldean order – this is simply the order of planets in decreasing apparent speed from Earth’s perspective: Saturn, Jupiter, Mars, Sun, Venus, Mercury, and Moon in that sequence. So for Thursday, the second hour would be ruled by Mars. The table below shows all the planetary hours for Thursday, and the first two for Friday – as can be seen, the natural Chaldean order means that the final night-time hour of Thursday is ruled by the Sun, so the next planet in the sequence – Venus – is the ruler of the first daytime hour of Friday, as one would expect for Dies Veneris.
Calculating all this in your head
Here’s a chart of an event, the Fall of the Berlin Wall, using Placidus houses. If you’re in front of a computer, you can find out the day easily enough, but if you’re sitting in a train reading an astrology book, it may not be so easy. Can you work out the Lord of the Day and the Lord of the Hour in your head by looking at this chart? Yes, you can!
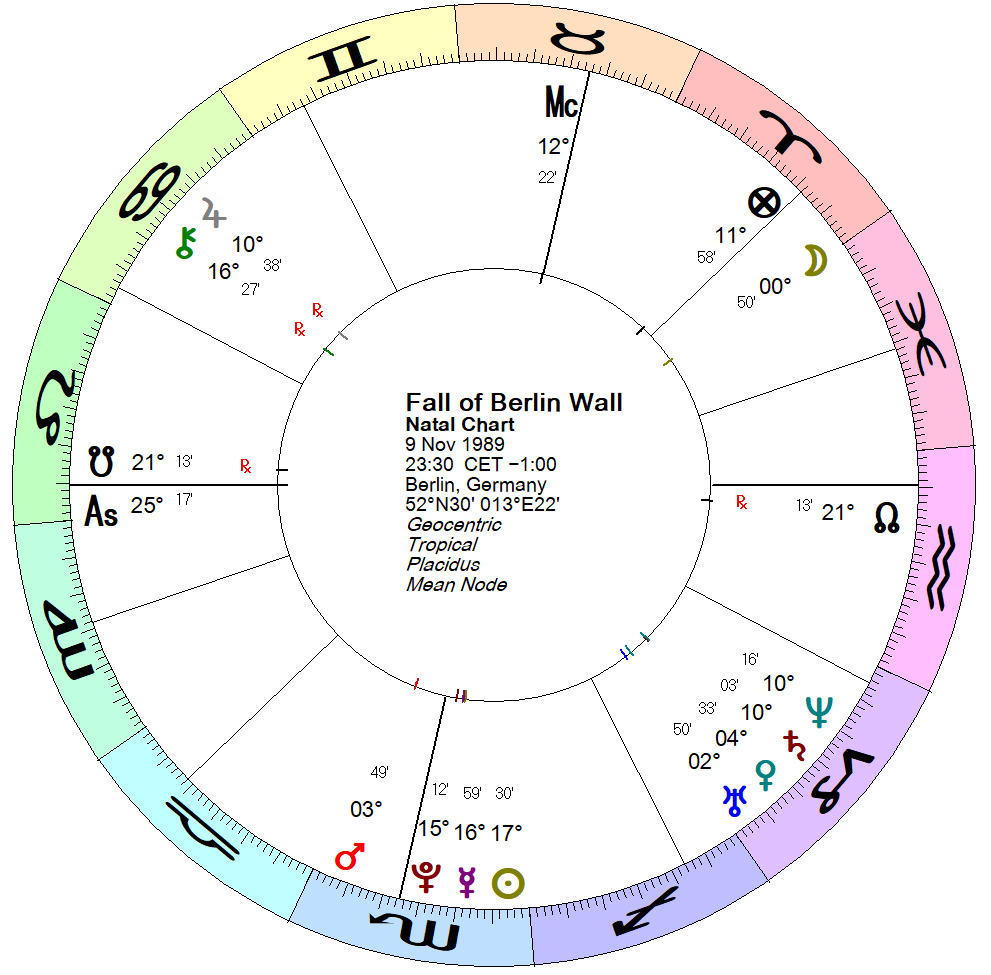
Fall of the Berlin Wall. Time set for the moment that Col Harald Jaeger opened the gates to let everyone through.
Lord of the Day
We know the event took place on 9 November 1989. What day was that – and how do you work this out in your head?
These instructions are a bit fiddly at first, but you only need to memorise the steps, and you’ll soon be able to work out any date if you’re reasonably good with numbers. A lot of the steps involve something called “modulo 7 arithmetic” – don’t be put off by the name, it just means that a lot of the steps involve dividing by 7 and just worrying about the remainder. So 10 divided by 7 is 1 with a remainder of 3. We’re only interested in that remainder – so 10 modulo 7 is 3. 22 modulo 7 is 1. 35 modulo 7 is 0 (because 7 goes into 35 exactly).
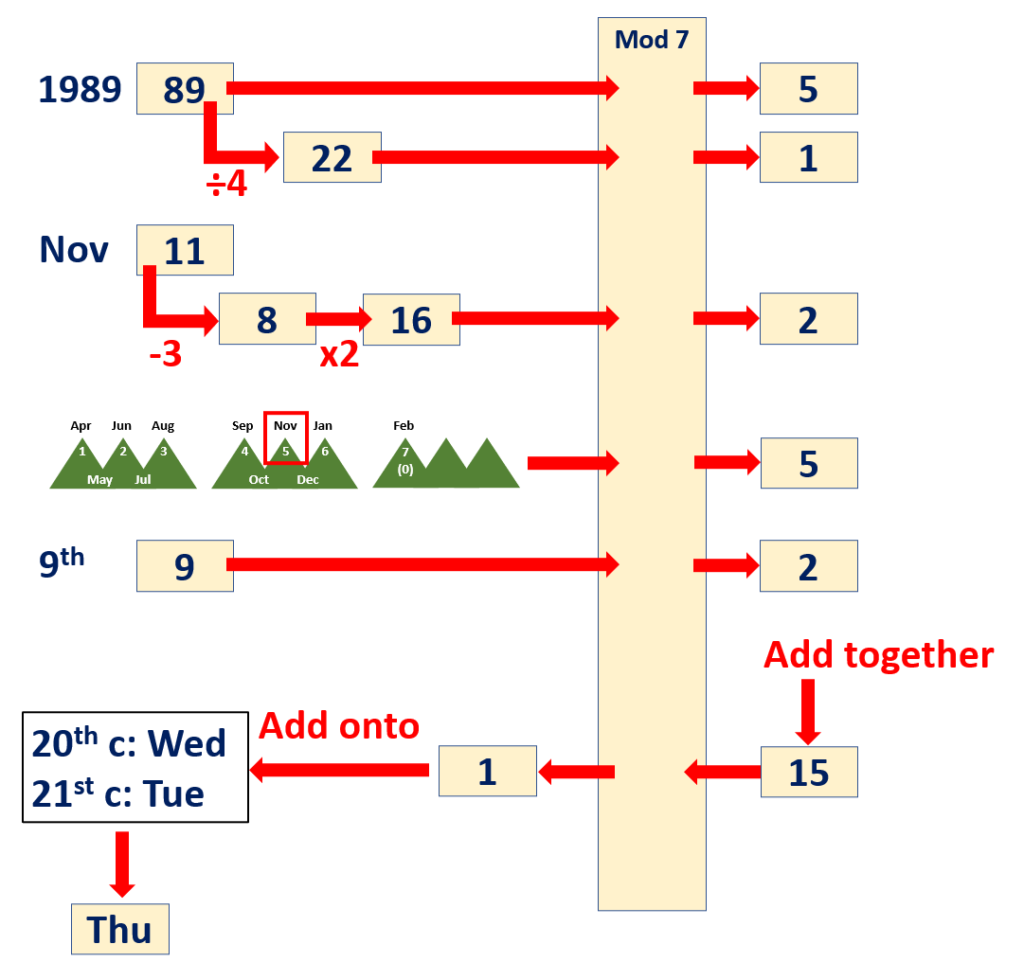
Start by noting the date, month, and year, but with this proviso: if the month is January or February, then instead of considering that the first and second months of the year, consider them the 13th and 14th months of the PREVIOUS year. I’ll do a second example shortly, but let’s start with 9 November 1989:
Start with the year: 1989, and just use the last two digits: 89
- What’s 89 modulo 7? 7 goes into 89 12 times, with a remainder of 5. Answer: 5.
- Now work out how many leap years there have been that century: divide 89 by 4 and ignore the remainder: 22. Take mod 7 of that and add to the answer above: 5 + 1 = 6.
- Now take the month number, subtract 3, and double it: November is month 11, subtract 3 is 8, double is 16. Take mod 7 of that and add to the answer above: 6 + 2 = 8. You’ll notice that for March, nothing is added (month 3 minus 3 is zero).
- Some months have 30 days, some have 31 (our trick of using February as the 14th month of the previous year means we can ignore the fiddly business of 28 or 29 days), in a semi-regular pattern. I think of this as three sets of mountain peaks, starting in April (I count these on my knuckles, just using the first three knuckles as “summits”) – see the diagram below. April is a summit, May is a dip, June is a summit, July is a dip, August is a summit. That’s the first three mountains. Now we use the second set: September is a summit, October is a dip, November is a summit, December is a dip, January is a summit. The third set of mountains is academic, actually – we’re only left with February as a summit. Then we see how many “summits” we’ve climbed – for November, it’s 5. I said February is academic, because that’s 7 – and 7 modulo 7 is zero, so we can skip this step completely for February. We can also skip it for March. Add that 5 onto our previous answer: 8 + 5 = 13.
- Then consider the date of the month – the 9th – do the modulo 7 of that and add to the previous answer: 13 + 2 = 15.
- Now take modulo 7 of that total to give us 1.
- This tells us how many days on from “day zero” we have to go; for the 20th century, “day zero” is Wednesday, and for the 21st century it’s Tuesday. This is a 20th-century date, so one day on from Wednesday is Thursday: 9 November 1989 was a Thursday.
Let’s try a second example: the Capitol riots on 6 January 2021. What day was that?
This is January, so we have to treat this as the 13th month of the previous year – 2020. So we use the last two digits of the year: 20.
- 20 mod 7 is 6 (7 goes into 20 twice, with a remainder of 6). Answer: 6.
- Divide 20 by 4 to find out how many leap years: 5. Add to previous answer: 11.
- Take the month number – this is 13 for January, subtract 3 and double it: 13 – 3 is 10, double is 20. Take mod 7 of that to get 6, and add to previous answer: 11 + 6 = 17.
- How many “summits” do we climb in our set of triple-peak mountains, starting with April? Count on your three of your knuckles and dips between knuckles: APRIL may JUNE july AUGUST – that’s three summits, and we’re not there yet. SEPTEMBER october NOVEMBER december JANUARY – we’re there, that’s another three summits, so six altogether. Add that to the previous answer: 17 + 6 = 23.
- Now consider the date of the month, the 6th – so add 6 to the answer to get 23 + 6 = 29.
- Take modulo 7 of that – 7 goes into 29 four times with a remainder of 1, so 1.
- This means we need to add one day onto our day zero for the 21st century – it was a Wednesday.
This seems fiddly, but you get the hang of it quite quickly – and it’s a great party trick!
Lord of the Hour
Lord of the Hour is easier to work out if you have a chart using Placidus houses in front of you.
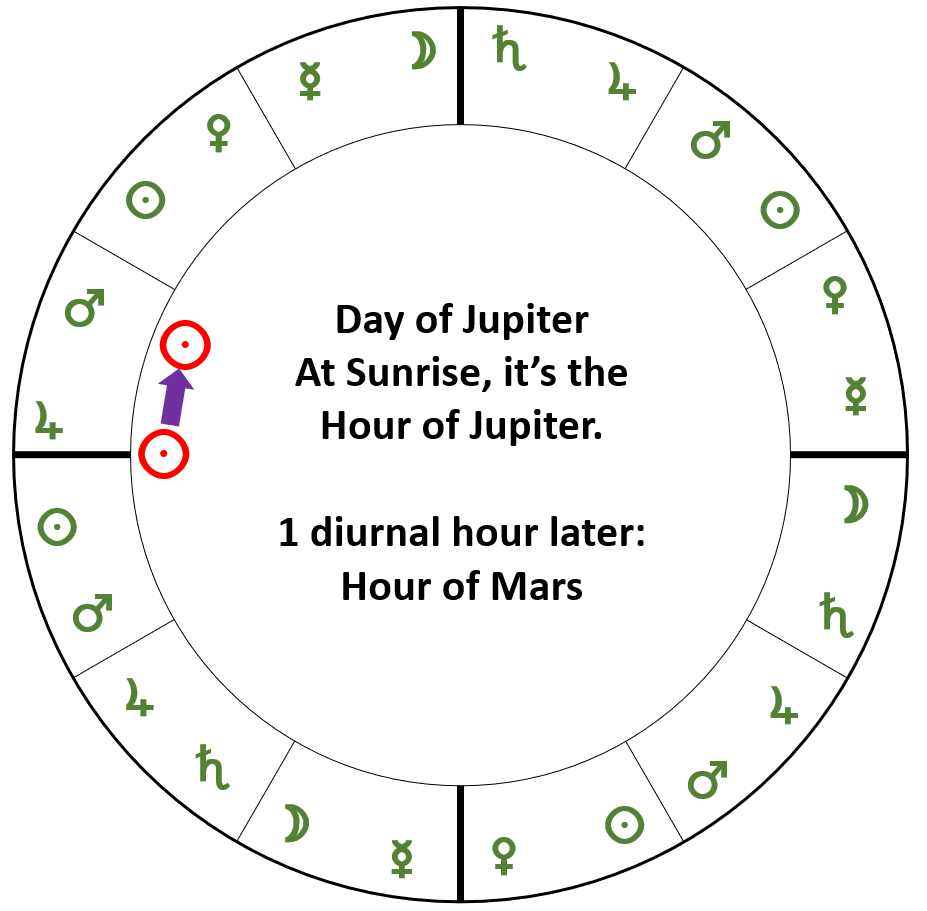
At sunrise, the Lord of the Hour is the same as the Lord of the Day. One diurnal hour later, the hour switches to the next planet in the Chaldean sequence. Take Thursday as an example – this is Jupiter’s day, so at sunrise the Lord of the Hour is Jupiter. One diurnal hour later, it’s Mars, then the Sun, then Venus and so on through a repeating cycle. As we saw above, working out diurnal hours can be quite tricky, but if you already have a chart in front of you, it’s easy (though the trick only works with Placidus houses – and I’m very grateful to Wade Caves for showing me this technique, and convincing me to return to Placidus as my usual house system!). Starting at the Ascendant and going clockwise (diurnal motion) divide each house in half and count the planets through the houses until you reach the point where the Sun is – on Thursday, the half of the 12th house nearest the Ascendant will be Jupiter, the upper half will be Mars, the bottom half of the 11th house is the Sun, the next half Venus and so on. In our example of the fall of the Berlin Wall, we can see the Sun in the bottom of the chart, and so counting from Jupiter at the Ascendant (since the day was a Thursday), we go round the houses until we reach the Sun, and can see that the Sun is at the position where Venus is the Lord of the Hour. This trick usually works, but if the Sun is very close to the middle of a house, you might still need to do the tricky sums to work it out for sure.
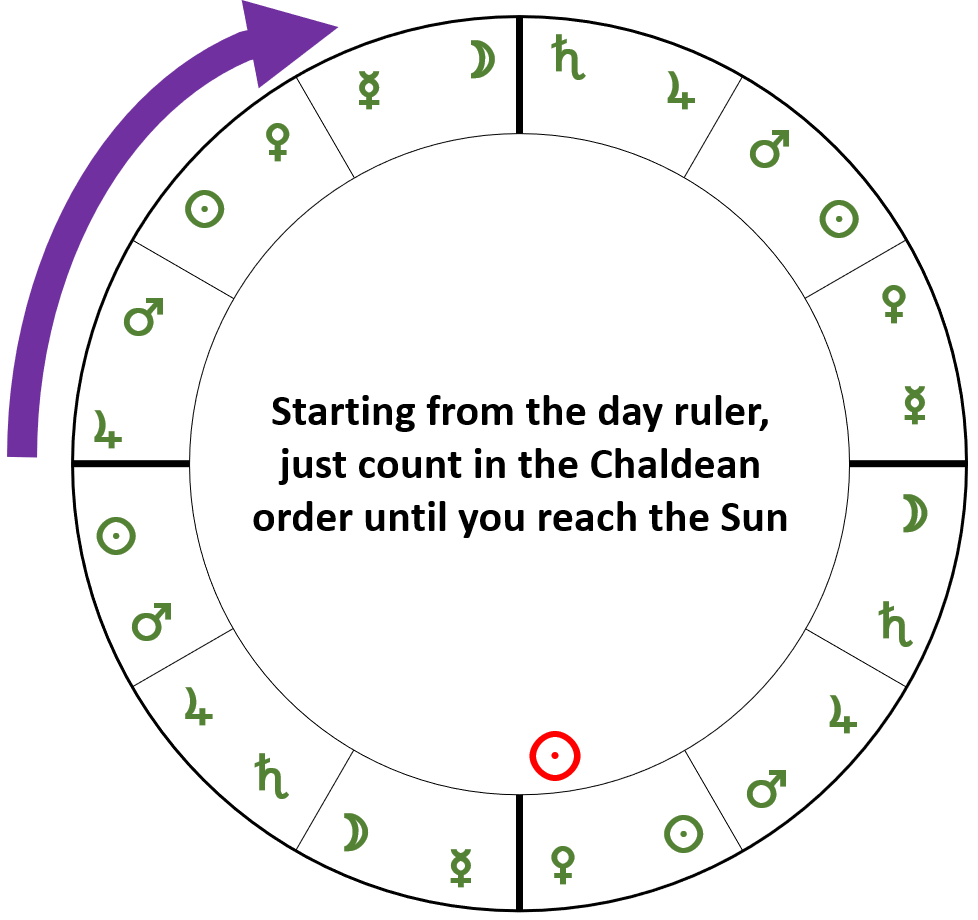
Also remember that a medieval day begins at sunrise. The chart above is set for 23:30 on Thursday 9 November 1989, showing Venus as Lord of the Hour. An hour later, the Sun would be in the third house in the section where Mercury is, so Mercury would be Lord of the Hour. However, because it’s after midnight, your software would give the date as 10 November 1989, a Friday – but medievally, because the Sun is still in the lower (nocturnal) half of the chart, you would have to pretend that it’s still 9 November, as the Lord of the Day doesn’t change until sunrise.
So next time you’re sitting on a train with an astrology book but no Internet connection looking at a chart and wondering what the Lord of the Day and Lord of the Hour is – you can do it in your head!